收藏级干货 | 充分搞懂高斯光束：从光束质量到透镜选型的全链路解析

导语

在激光光学系统的设计中，我们常常会遇到一个令人头疼的现象：

明明按照几何光学公式1/f = 1/s + 1/s’计算好了透镜位置，为什么实际测量到的光斑大小和位置总是有偏差？为什么想把光斑聚焦得更小，却发现焦深变得极短？

答案在于：激光不是直线，而是波。

大多数激光应用都假设光束是理想的高斯光束（Gaussian Beam）。它的传播规律、聚焦特性与我们熟悉的传统成像光学大相径庭。如果继续沿用简单的几何光学思维，你的激光系统设计注定会存在误差。

今天，我们将基于经典教程，深入剖析高斯光束的传播机理、薄透镜公式修正以及“焦距变换"这一反直觉现象。



01 什么是真正的高斯光束？

The Anatomy of a Gaussian Beam

当我们谈论激光束时，我们首先要明确它的能量分布。理想的基模激光束（TEM00）其辐照度分布是轴对称的，且随着离轴距离的增加呈高斯函数衰减。

但在工程实践中，没有真正的理想光束。我们通常引入 M²因子（光束质量因子） 来描述真实激光束与衍射极限下的理想高斯光束的差距。

一个理想高斯光束的辐照度分布公式如下：



这里有一个关键概念：光束半径 w(z）。

它并不是光束的“边缘"，而是指辐照度下降到峰值 I0的 1/e²（约13.5%）处的径向距离。

图1: 高斯光束的束腰定义为辐照度为其较大值1/e2 (13.5%) 的位置

02 束腰、发散与瑞利长度

Understanding Propagation Parameters

激光束在空间传播时，其直径并不是恒定的。受衍射效应影响，光束会经历“收敛-束腰-发散"的过程。

• 束腰 (Beam Waist, w₀)：光束直径最小的位置。

• 发散角 (Divergence, θ)：描述光束在远场扩散程度的参数。

这两者之间存在着一个类似于“测不准原理"的制约关系：

 

划重点： 束腰越小，发散角越大；束腰越大，光束准直性越好。这就是为什么激光扩束镜通过放大光束直径，反而能获得更准直光束的物理原因。

此外，还有一个工程师必须掌握的参数——瑞利长度 (zR)。

它定义了光束横截面积增加到束腰处两倍（即直径增加到 √2 w₀）时的轴向距离。

 

瑞利长度决定了激光加工中的焦深（Depth of Focus）。如果你需要切割厚材料，你不仅需要极小的光斑，还需要足够长的瑞利长度。

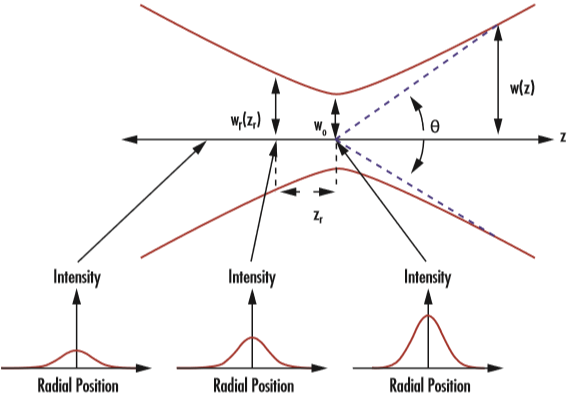
图2: 高斯光束通过其束腰 (w0)、瑞利长度 (zR) 和发散角 (θ) 定义

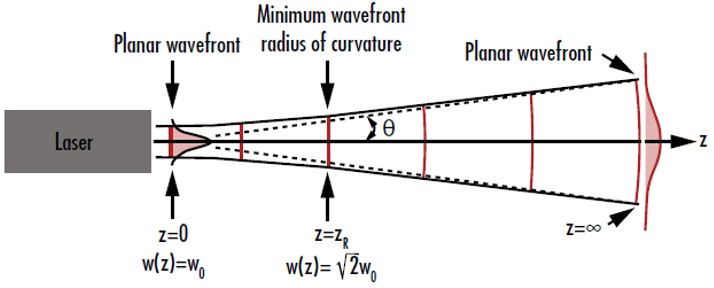
图3: 当高斯光束离束腰非常近和非常远时，其波前曲率接近于零



03 修正：高斯光束的薄透镜公式

The Gaussian Thin Lens Equation

这是最容易“翻车"的地方。

在传统成像光学中，我们使用公式

但在激光光学中，我们需要引入Sidney Self在1983年推导的高斯薄透镜公式：

 

• s：输入束腰到透镜的距离

• s’：透镜到输出束腰的距离

• f：透镜焦距

注意： 当瑞利长度zR趋近于0时，这个公式才退化为我们熟悉的几何光学公式。对于长焦距透镜或大光斑系统，直接套用几何公式会导致焦平面位置计算严重偏差。

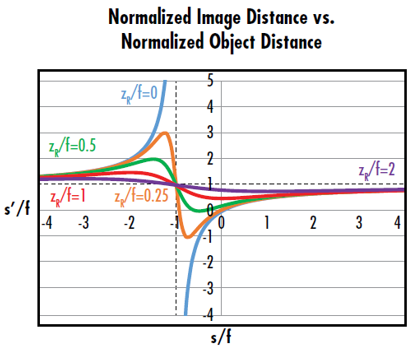
图4: zR/f=0 的曲线对应于传统的薄透镜公式。zR/f>0 的曲线表 明，高斯成像具有瑞利长度所定义的最小和较大成像距离

为了简化计算，我们通常引入放大倍率 α：

 

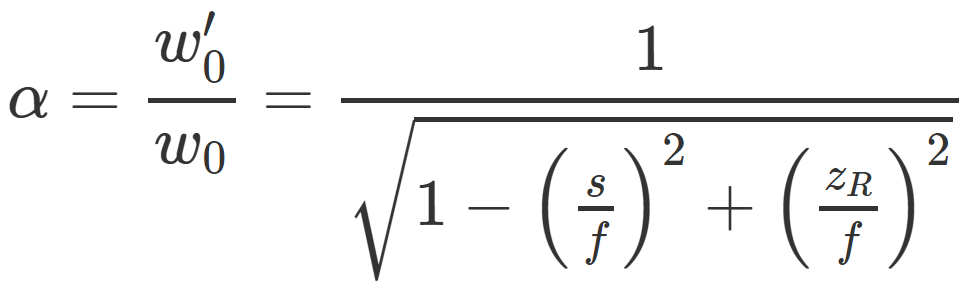
掌握了这个倍率，你就可以算出透镜后的新束腰大小w₀'和新瑞利长度zR'。



04 实战：如何获得最小的聚焦光斑？

Focusing a Laser Beam to a Spot

在激光打标、切割或手术应用中，我们的核心目标通常只有一个：把能量集中在尽可能小的点上。

根据推导，输出束腰w₀'的计算公式为：

 

如何让 w₀'最小？观察公式分母，我们需要较大化分母。这意味着：

1.减小焦距f：使用短焦透镜。

2.增大输入光束直径：在聚焦透镜前加装扩束镜。

这里有两种极限情况的简化算法，非常适合工程估算：

情况 A：透镜在瑞利范围内 (s ≪ zR)此时，输出束腰简化为：



这再次印证了：输入光斑 w₀越大，聚焦光斑w₀'越小。

情况 B：透镜远离瑞利范围 (s ≫ zR)此时，输出束腰简化为：



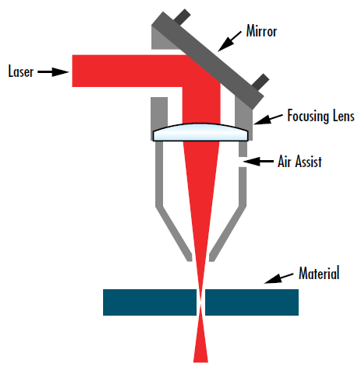
图5: 将激光束聚焦到尽可能小的尺寸对于包括这种激光切割装置在内的广泛应用至关重要

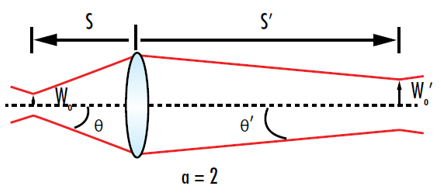
图6: 对于放大倍率2，输出束腰将是输入束腰的两倍，输出发散将是输入光束发散的一半



05 反直觉现象：高斯焦距变换

Gaussian Focal Shift

这是一个经常困扰新手的问题：光强较大的点，真的在透镜的几何焦点上吗？

答案是：不一定。

这种现象被称为高斯焦距变换（Gaussian Focal Shift）。

当我们将高斯光束聚焦时，光束半径最小的位置（即实际束腰位置）通常会稍微偏向透镜一侧，而不是落在几何焦距f处。

虽然在大多数高频应用中这个偏移量很小，但在精密测量或微纳加工中，这个微小的Δz足以影响加工质量。

最/大光强位置≠几何焦点

只有当输入光束近似为准直光（s趋向于无穷大）或聚焦在束腰附近时，最小光斑位置才会与几何焦点重合。

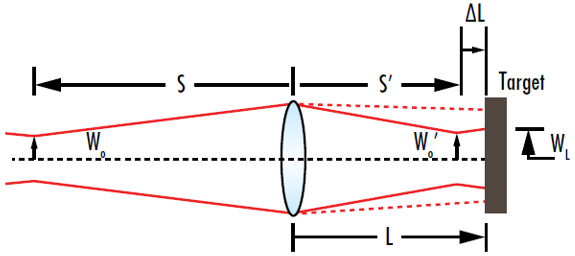
图7: 目标处的光束半径在聚焦光束的束腰出现在目标前的特定位置，而不是目标处时达到最小值



结尾

高斯光束的传播并非玄学，而是遵循着严谨的物理与数+学规律。

从 M²因子的评估，到薄透镜公式的修正，再到对焦距变换的理解，每一个细节都决定了激光系统的最终性能。在设计光学系统时，切记不能简单地将激光等同于几何光线。

总结一下今天的关键点：

1.激光束腰与发散角成反比。

2.计算激光聚焦位置时，请使用高斯薄透镜公式，而非几何光学公式。

3.想要更小的聚焦光斑？请缩短焦距或扩大入射光束。

4.警惕“焦距变换"，实际焦点可能比你计算的更靠近透镜。